KLASA 1
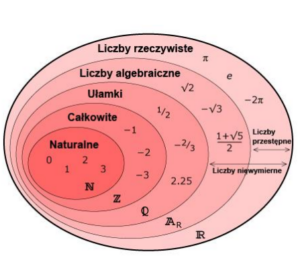
Liczby naturalne, całkowite, wymierne, niewymierne
Liczby naturalne
Liczby naturalne to liczby, które są dodatnie i całkowite: 0, 1, 2, 3, 4, 5, ….
- Zbiór liczb naturalnych oznaczamy symbolem ℕ.
Przykład:
- Liczby naturalne większe od 3 i mniejsze od 7 to: 4, 5, 6.
Cechy podzielności liczb
Cechy podzielności pomagają nam szybko sprawdzić, czy liczba dzieli się przez inną liczbę bez wykonywania dzielenia.
- Podzielność przez 2: Liczba jest podzielna przez 2, jeśli jej ostatnia cyfra to 0, 2, 4, 6 lub 8.
Przykład: 24 jest podzielne przez 2, bo kończy się na 4. - Podzielność przez 3: Liczba jest podzielna przez 3, jeśli suma jej cyfr jest podzielna przez 3.
Przykład: 123 jest podzielne przez 3, bo 1 + 2 + 3 = 6, a 6 dzieli się przez - Podzielność przez 4: Liczba jest podzielna przez 4, jeśli liczba utworzona z jej dwóch ostatnich cyfr jest podzielna przez 4.
- Podzielność przez 5: Liczba jest podzielna przez 5, jeśli jej ostatnia cyfra to 0 lub 5.
Przykład: 50 jest podzielne przez 5, bo kończy się na 0. - Podzielność przez 6: Liczba jest podzielna przez 6, jeśli jest podzielna zarówno przez 2, jak i przez 3.Przykład: 24 jest podzielne przez 6, bo jest podzielne przez 2 (kończy się na 4) i przez 3 (2 + 4 = 6, a 6 dzieli się przez 3).
- Podzielność przez 9: Liczba jest podzielna przez 9, jeśli suma jej cyfr jest podzielna przez 9.
Przykład: 126 jest podzielne przez 9, bo 1 + 2 + 6 = 9, a 9 dzieli się przez 9.
Podzielność przez 10: Liczba jest podzielna przez 10, jeśli jej ostatnia cyfra to 0.
Przykład: 100 jest podzielne przez 10, bo kończy się na 0.
- Podzielność przez 2: Liczba jest podzielna przez 2, jeśli jej ostatnia cyfra to 0, 2, 4, 6 lub 8.
Liczby całkowite
Liczby całkowite to liczby naturalne oraz ich ujemne odpowiedniki i zero: …, -3, -2, -1, 0, 1, 2, 3, ….
- Zbiór liczb całkowitych oznaczamy symbolem ℤ.
Przykład:
- Liczby całkowite większe od -3 i mniejsze od 2 to: -2, -1, 0, 1.
Liczby wymierne
Liczby wymierne to liczby, które można zapisać w postaci ułamka zwykłego abba, gdzie a i b są liczbami całkowitymi, a b ≠ 0.
- Zbiór liczb wymiernych oznaczamy symbolem ℚ.
- Liczby wymierne obejmują zarówno ułamki skończone, jak i ułamki okresowe.
Przykłady:
- 1221 = 0,5 (ułamek skończony).
- 1331 = 0,333… (ułamek okresowy).
Liczby niewymierne
Liczby niewymierne to liczby, których nie da się zapisać jako ułamek zwykły. Mają one nieskończone i nieokresowe rozwinięcie dziesiętne.
- Przykłady liczb niewymiernych: √2, π, e.
Przykład:
- √2 ≈ 1,41421356… – to rozwinięcie nigdy się nie kończy i nie ma okresu.
Liczby rzeczywiste
Liczby rzeczywiste to wszystkie liczby, które możemy znaleźć na osi liczbowej. Obejmują one zarówno liczby wymierne, jak i niewymierne.
- Zbiór liczb rzeczywistych oznaczamy symbolem ℝ.
Liczby pierwsze
Liczby pierwsze to liczby naturalne większe od 1, które mają dokładnie dwa różne dzielniki: 1 i samą siebie.
- Liczby pierwsze są jak “cegiełki” w matematyce, ponieważ każdą liczbę naturalną większą od 1 można zapisać jako iloczyn liczb pierwszych (tzw. rozkład na czynniki pierwsze).
- Najmniejszą liczbą pierwszą jest 2 (to jedyna parzysta liczba pierwsza).
Przykłady liczb pierwszych:
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …
Liczby złożone
Liczby złożone to liczby naturalne większe od 1, które mają więcej niż dwa dzielniki.
- Innymi słowy, liczby złożone można rozłożyć na iloczyn mniejszych liczb naturalnych (np. 4 = 2 × 2).
- Każda liczba złożona ma co najmniej jeden dzielnik pierwszy.
Przykłady liczb złożonych:
- 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, …
Ciekawostka:
Liczba 0 i 1 nie są ani pierwsze, ani złożone.
Praca domowa:
1. Wypisz wszystkie liczby całkowite większe od -4 i mniejsze od 3.
2. Sprawdź, czy liczba 246 jest podzielna przez 6.
3. Które z poniższych liczb są niewymierne?
a) 0,125
b) π
c) 2552
4. Wypisz wszystkie liczby pierwsze większe od 10 i mniejsze od 20.Wypisz wszystkie liczby złożone większe od 15 i mniejsze od 25.
5. Sprawdź, czy liczba 29 jest liczbą pierwszą.
6. Rozłóż liczbę 36 na czynniki pierwsze.
- Strona główna
- Cennik
- Szkoła podstawowa
- Szkoła średnia
- Klasa I
- 1.1 Liczby rzeczywiste
- 1.1.1 Liczby naturalne, całkowite, wymierne, niewymierne
- 1.1.2 Rozwinięcie dziesiętne liczby rzeczywistej
- 1.1.3 Pierwiastek kwadratowy i sześcienny
- 1.1.4 Potęga o wykładniku całkowitym oraz notacja wykładnicza
- 1.1.5 Potęga o wykładniku wymiernym
- 1.1.6 Logarytm i jego własności
- 1.1.7 Procenty
- 1.1.8 Powtórzenie
- 1.2 Język matematyki
- 1.3 Układy równań
- 1.4 Funkcje
- 1.5 Funkcja liniowa
- 1.6 Planimetria
- 1.7 Funkcja kwadratowa
- 1.1 Liczby rzeczywiste
- Klasa II
- Klasa III
- Klasa IV
- Matura
- Klasa I
- Kontakt
- Kalendarz